Q9 パーシェ方式の基本の考え方は?
基準時点と比較時点の購入数量を固定して両時点の買い物かごの合計代金を比べるのが、もともとの物価指数の計算方法。
ラスパイレスさんは「基準時点の数量が比較時点にも変わらない」という仮定の計算にしましたが、パーシェさんは「比較時点の数量が基準時点にも変わらない」と仮定しました。
これによって、「価格が上がったら買い控え、価格が下がったら多く買う」という消費者の行動が計算に反映されることにはなりました。
例によって、果物物価指数モデルで考えます。単価は前回と同じく、「ミカンは50円→40円、リンゴは100円→130円、バナナは50円で変わらず」です。前回は、「基準時点の数量で固定し、その数量はミカン10個、リンゴ3個、バナナ4本」としました。
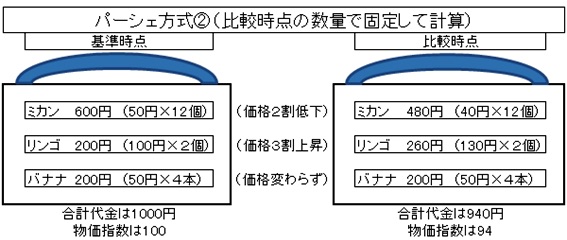
今回は、パーシェ方式で計算するため、「比較時点の数量で固定し、その数量はミカン12個、リンゴ2個、バナナ4本」と仮定します。値下がりしたミカンの購入数量を増やして値上がりしたリンゴの購入数量を減らしてみたわけです。
図の通り、合計代金は、基準時点1000円、比較時点940円となります。物価指数は、100→94の推移。この図を見てじっくり考えると分かりますが、比較時点の数量で固定するというルールがあるなら、数量を無視して、各品目の比較時点の代金をもとに価格変化率を反映させて基準時点の各品目の代金を計算することができます。
比較時点の代金は、ミカン480円、リンゴ260円。ミカンは「480円÷0.8」つまり「480円×1.25」で基準時点は600円。リンゴは「260円÷1.3」つまり「260円×0.77」で基準時点は200円というわけです。
パーシェ方式で計算しても物価指数の変化率が正しく計算できるわけではありません。前回と今回の果物物価指数モデルのミカンの購入個数を思い出してください。
「モデルの中の現実」では、基準時点は10個で比較時点は12個でした。ラスパイレス方式のときは、基準時点の個数で固定するので、基準時点と比較時点とも10個。
一方、パーシェ方式では比較時点の個数で固定するので、両時点とも12個。両方式とも現実とずれていますね。
厳密な正解は両方式の間にあると考えられています。両方式には一長一短があるのです。

